"Chapter. 0 - 함수의 연속"
“Chapter. 0 – 함수의 연속”
안녕하세요 ‘한국외대 부’입니다. 언제나 여러분 입시에 가장 먼저 앞서있고,
길을 내주는 길잡이가 되어드리도록 최선을 다해 앞장서겠습니다!
오늘의 제목은 “함수의 연속”입니다. 모든 칼럼은 저의 자료의 내용으로 진행됩니다!
수2 내용의 함수 파트는 22번 15번 등으로 킬러로 자주 등장하는 내용입니다.
오늘은 킬러로 자주 등장하는 ‘함수의 연속’에 대해 알아봅시다.
함수의 연속은 함수를 결정하는데 중요한 조건이 됩니다.
수2에선 초월함수가 등장하지 않아 ‘연속’이라는 조건 만으로도 많은 정보를 알 수 있습니다!
특히, 수2에선 다항함수가 자주 출현하기에 연속과 미분 가능성에 대해서 항상 주의깊게 확인해야합니다.
연속임을 확인하는 방법은 정말 단순합니다.

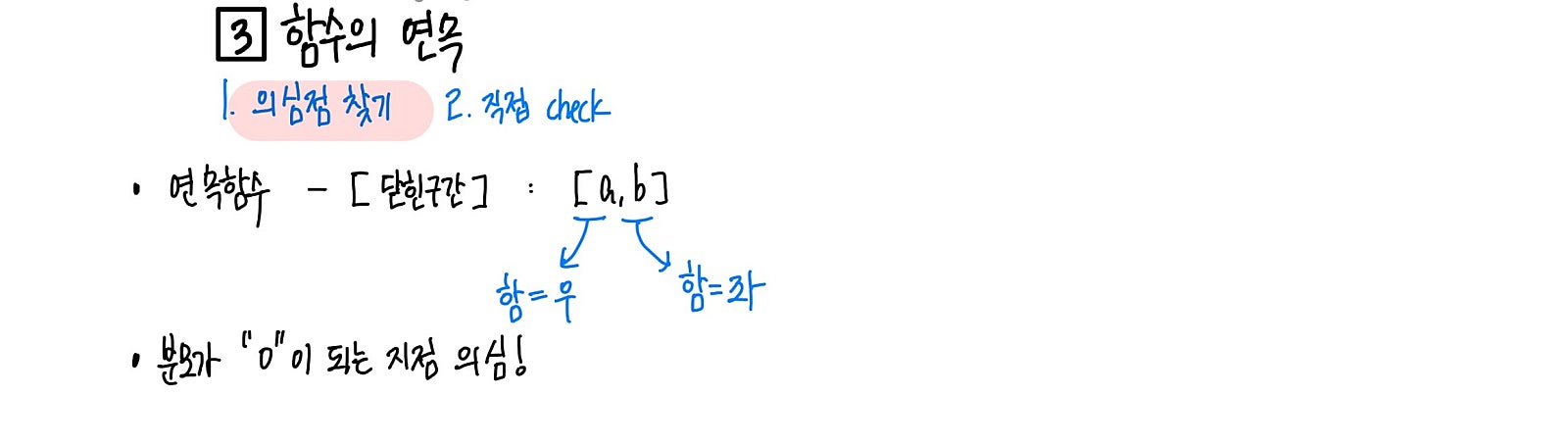
함수의 연속을 확인하는 의심점 찾는 방법을 확인해주세요.
먼저, 의심되는 지점에서 연속이 되는지만 확인하면 됩니다!
그 의심되는 지점을 어떻게 찾는지 알아봅시다.
첫 번째, 경계를 의심하자!
단순히 설명된 연속함수의 경우 닫힌 구간으로 정의된 그 경계가 의심점이 됩니다.
경계로 정의된 함수의 경우 경계 사이는 대부분 연속되는 구간으로 주어지고 그 경계에서 다른 함수로 바뀌거나 새로운 조건이 붙는 경우가 많습니다.
두 번째, 분모가 “0”이되는 지점을 의심하자!
분수로 표현된 유리함수의 경우 분모가 0인 지점을 항상 의심해야 합니다.
그 지점은 존재 자체를 안하기에 분모가 0이되는 좌,우 극한의 값과 같은 값을 지니는
다른 함수의 값으로 표현되어야 연속이 됩니다.
마지막으로, 합성함수의 연속에 대해 알아봅시다!

합성함수는 그 주인공이 무조건! 겉함수입니다.
그림과 함께 보면 합성함수는 두 개의 함수를 합성 시켜놓은 꼴이기에
두 개의 함수의 연속 의심지점을 모두 고려해야 합니다.
따라서 이와같이 속함수에서 겉함수로 넘어가는 부분을 꼼꼼히 체크해야합니다.
어느하나 빠지지 않게 잘 체크하여 그 좌,우극한 값과 함수값이 같은지 확인해야합니다.
합성함수의 연속을 잘 이해했나 확인해보기 위해
2016년 6월 모의고사 문제를 예시로 같이 풀어봅시다.


앞의 합성함수의 연속을 확인 하는 방법을 같이 보면서 해설을 읽어주세요!
속함수의 연속의 조건에서 경계인 x=1에서의 좌,우,함수값을 모두 의심해야하며,
그 값을 정의역으로 하는 g(x)에서의 값이 모두 동일해야하니
g(a)값은 g(1)의 값과 같아야 합니다, 따라서 이를 만족시키는 a의 모든 값의 곱은 1과 –1의곱인 –1입니다.
합성함수를 관찰할 때 중요하게 봐야하는 부분은
속함수의 치역이 겉함수의 정의역이 된다는 점입니다.
이점은 아직 미숙할지 몰라도 여러 예시 문항들을 풀어보면서 꾸준히 연습해야 합니다.
오늘의 내용은 여기까지 입니다!
앞으로 더 많은 내용들로 꾸준히 찾아올테니 좋아요과 구독 한번씩만 눌러주시고 기다려주세요!
자료의 전체버전은
https://cafe.naver.com/suhui/28704323 에서 확인해주세요!
고민이나 공부상담, 원하시는 칼럼의 내용이 있으시면 댓글이나 쪽지로 남겨주세요.
다음 칼럼에 반영하여 작성하겠습니다!
수험생의 길잡이가 되어드리는
'한국외대 부'였습니다 감사합니다!
0 XDK (+0)
유익한 글을 읽었다면 작성자에게 XDK를 선물하세요.
-

 좋아요 0 답글 달기 신고
좋아요 0 답글 달기 신고
-
한양대생 소환술 3
"하냥대? 송하냥밖에 모르는데?" "어 거기 에리카 이원화 아니야?"
-
조절 실패햇어 어카냔 ㅏ나
-
관리 엄청 잘하신 90년대생분들이 많네..
-
제발.. 내가 집을 지키겟네.. 일하기 싫어..
-
전 계정은 일찍 만들어뒀는데 고등학교 2학년 말 쯤에 수능 관련 정보 구글에...
-
정말 자야만해 0
죽기 싫어
-
저도이제잘게요 5
옯친구들 다들 잘장
-
1단원 문제 3개 투척! 풀이해주시면 1000덕 드림
-
대존맛임뇨
-
저한테 버려주실 분 9함뇨 저는 덕코를 드리겠습니다
-
성대생 소환술 3
"응 니네 이과 싹 다 유배" "서성한중"
-
시이발
-
혹시 저에게 하는 말이라고 이해해도 될까요?아니오 주어는 없습니다 :)
-
제발 제 잡담 태그를 꺼주세요 얘 ㄹㅇ 쓸모없는 글만 하루에 20개 쓰고 쓸모 있는...
-
작년 12월인가 인스타 현우진꺼 보고있었는데 스토리로 누굴 저격하는거임 ㅋㅋㅋ...
-
오르비 1
내리비 오르락내리락 반복돼 기쁨과 슬픔이 반복돼~
-
수1 수2 둘 다 들으려고 하고 개념 꼼꼼히 설명해주는 강사보다 팁 주고 강의 수...
-
김상훈 6
문학론이랑 문학 개념 매뉴얼 중에 뭐 해야하나요? 둘다 해여하나요?
-
케리아랑 좀 비슷하다 자꾸 겹쳐보인다
-
성적도 안좋은데 뻘글이나 싸지른 중게이라 ㅈㅅㅎㄴㄷ
-
논리실증주의자는 예측이 맞을 경우에, 포퍼는 예측이 틀리지 않는 한, 4
논리싫증주의자는 관심이 없다
-
정병걸리는 학생 0
-
[칼럼] 어떻게 해야 오르비에 잘 적응할 수 있는가 13
여기에는 여러가지 방법이 있으나 본인이 아는 대표적인 방법을 알려주고자 한다. 1....
-
대학커뮤니티 노크에서 선발한 한양대 선배가 오르비에 있는 예비 한양대학생, 한양대...
-
대학커뮤니티 노크에서 선발한 이화여대 선배가 오르비에 있는 예비 이화여대학생,...
-
미적투표 4
26수능 시험지에서 보고싶은 문항배치는??
-
수특 출고 예정일 12
화1이 왜 과탐 1위 입고 엌
-
No를 쓰는게 아니라구요!!!!!
-
이거 맞음?? 뭔 중세 성같네
-
초단타 1
내일 점심값 굳었다
-
캬하하하
-
모고3~4등급(고2)정도 뜨고 확통입니다. 이번에 선생님과 상담하다가 정승제...
-
유튜브 댓글에서 강k가 평가원보다 퀄리티가 더 좋다던대 진짜임?
-
이것저것 해보긴 했는데.. 학교다니면서 하려면 편의점같은게 낫겠지 가르치는데...
-
당사자의 추가입장입니다 24
근데 댓글 보면서 느끼는게 예시로 든거 같고 사실관계가 틀리다니... 나한테 한...
-
솔직히 좀 편했음ㅋㅋ 올해도 안나왔으면 하는데
-
시대 자료 다 자기가 이름짓는다고... 그런김에 서바모음도 뿌려줘요
-
내가 S면 넌 나의 11
EX가 되어줘
-
진짜 잘생기긴했다
-
포폴과 자본의 중요함 like 덕코 용돈 마싰다
-
시대인재 두각 세정 같은곳 말고 내신때문에 꽤 있을려나
-
1. 소설에서의 장면나누기 관련 칼럼 2. 최근 이슈화된 문학 선지들 뜯어보기 칼럼...
-
나 궁금해 죽을거 같아
-
수고해
-
평소보다 빨리 취하나요? 정신은 차릴수있는데 존나 어지러운데 500ml 6분인가7분컷함




















































